При изучении элементарной геометрии необходимо точно определить, что именно мы будем изучать. Каждая наука ставит в центр внимания определенные объекты, или понятия, которые должны быть четко и однозначно определены. Это нужно, чтобы у оппонентов не возникало причин для оспаривания полученных в ходе эксперимента или теоретических разработок выводов.
Геометрии это касается в полной мере. Это одна из самых древних наук, возникшая из необходимости измерения площадей земельных участков, длины пути, расстояния между городами. Позже предметом прикладной геометрии стали архитектурные проекты, определение положения звезд и вычисление размеров земли. Но сугубо прикладных функций, полезных в повседневной жизни, она не утратила.
Геометрические фигуры
Первый вопрос, на который нужно ответить при изучении раздела, является ли точка геометрической фигурой? Ответ сформулировал еще Эвклид — точка, это простейшая фигура, элемент, из которого состоят все остальные фигуры. Линия, как ошибочно думают многие, не элементарная фигура, а совокупность точек.
Из точек состоят все простые и сложные геометрические построения. Это единственная фигура, размеры которой нельзя определить и указать, как нельзя и ничего определенного сказать о количестве точек в длинной или короткой линии, как нельзя определить с достаточно высокой точностью количество атомов в массивном бесформенном куске железа или камня.
Название геометрических тел
Простейшие фигуры
Из точек можно создать любые линии, прямые, закругленные, зигзагообразные. Вариантов множество. Линия — вторая по простоте фигура после точки. Все линии подразделяются на несколько видов:
Прямая — бесконечная последовательность точек, определяющая кратчайшее расстояние между двумя произвольными точками. Крайние пункты могут быть расположены как на расстоянии в несколько миллиметров, так и на противоположных концах Вселенной. Но важно одно, прямая проходит через эти точки и стремиться дальше, ни начала, ни конца у нее нет.
Отрезок — частичный случай прямой. Это то же расстояние между двумя точками, но линия начинается на одной из них, и заканчивается на другой. Длина отрезка — величина вполне определенная измеряемая при помощи линейки, циркуля или рулетки, в зависимости от того, где находится данный отрезок.
Луч — часть прямой, лежащая по одну сторону от выбранной точки. Луч имеет начало, но не имеет конца. Как пример геометрического луча можно привести луч фонарика или лазерной указки. Началом является лампочка или светодиод, а дальше луч распространяется как угодно далеко.
Ломаная линия — совокупность отрезков, которые имеют по одной общей точке (начало следующего отрезка является концом предыдущего), но не лежат на одной прямой. Ломаная линия может быть как замкнутой, так и незамкнутой. Если линия замкнута, то образует другой геометрический объект — плоскую фигуру.
Дуга — совокупность точек, которые находятся на одной линии, но не на одной прямой. Частичный случай — фрагмент окружности.
Как уже говорилось, замкнутые ломаные линии образуют плоские фигуры. Почему плоские, мы рассматриваем только линии, которые находятся в системе координат XY, то есть, всех их можно нарисовать на листе бумаги не прибегая к такой сложной технике, как перспектива.
Треугольник — самая простая и самая устойчивая плоская фигура. Образована тремя отрезками, соединенными последовательно. Чтобы построить треугольник, необходимо, чтобы сумма длин любых двух отрезков превышала длину третьего. В зависимости от длин отрезков и углов между ними, треугольники подразделяются на равносторонние, равнобедренные, прямоугольные и произвольные (с тупыми и острыми углами).
Четырехугольники
Квадрат — фигура из четырех отрезков равной длины, углы между которыми равны 90о.
Прямоугольник — составленная из четырех отрезков, расположенных под углом в 90 о, но длины их равны попарно, то есть на противоположных сторона фигуры находятся равные отрезки.
Параллелограмм — четырехугольник, составленных из таких же отрезков, как и прямоугольник, но углы не равны 90о.
Ромб — преобразованный квадрат. Длина всех сторон одинакова, но углы не прямые. Иногда квадрат называют прямоугольным ромбом.
Трапеция — фигура, у которой параллельны только две противоположные стороны, которые называют основанием. В зависимости от расположения двух оставшихся сторон, трапеция бывает прямоугольной и непрямоугольной.
Многоугольники
Назвать все виды фигур в геометрии очень сложно. Но необходимо назвать многоугольники — это категория фигур, у которых количество сторон более 4. Их так и называют — пятиугольник, шестиугольник, восьмиугольник. В научной литературе многоугольники получили название «полигон». Соответственно, пятиугольник — пентагон, восьмиугольник — октагон и т.д.
Круги и овалы
Это фигуры, которые состоят не из отрезков, а из последовательно расположенных точек, находящихся на определенном расстоянии от центра. У кругов это расстояние одинаковое, у овалов — разное.
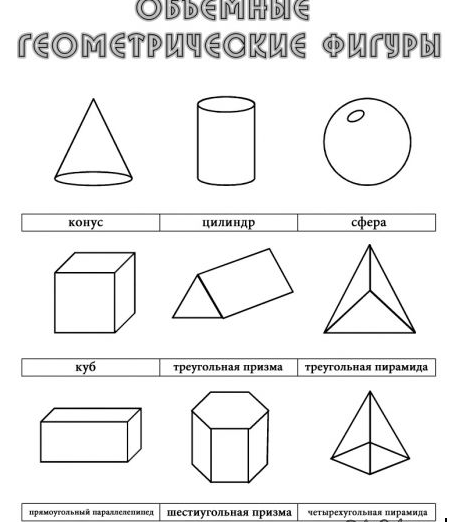
Объемные фигуры
Если рассматривать геометрические построения в пространстве координат XYZ, то получаются объемные фигуры, или тела. Это куб, конус, цилиндр, шар и другие. Но их изучение — предмет другой темы.